Fulsome & Canonical
One of the major difficulties when constructing algorithms for the rectilinear Steiner Tree Problem is that there in general exists an infinite number of RSMTs for a given terminal set Z.One RSMT may be transformed into another RSMT by performing so-called sliding and flipping operations that do not change the length of the tree.
In order to limit the number of RSMTs to be considered we will give a particular characterization of RSMTs that turns out to be very strong. Thus all RSMTs that do not fulfill the properties of this characterization will be ignored.
A rectilinear Steiner tree in which every terminal is a leaf is denoted a full Steiner tree or FST.
Every SMT is a union of FSTs.
Fulsome RSMT
A fulsome SMT is an SMT in which the number of FSTs is maximized. In particular no FST in a fulsome SMT can be split into two or more FSTs.
Canonical RSMT
A RSMT is canonical if no segment can be moved to the right using sliding and/or flipping operations.
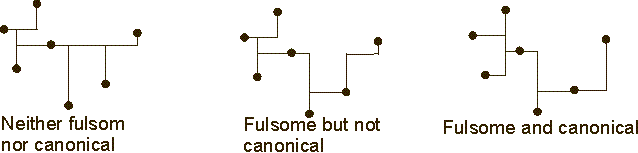
Figure 9:Transformation to fulsome and canonical
Flipping
When a path connects a point A(x1, y1) and a point B(x2, y2), where x1 ≠ x2 and y1 ≠ y2, the path consists of a vertical line and a horizontal line. The length of the path is |x2-x1|+|y2-y1|. The length does not change whether the path goes in the vertical direction first and then in the horizontal direction or it goes first in the horizontal direction and then in the vertical direction.
Flipping is the operation of altering the sequence of horizontal and vertical lines that make up the path between A and B.
Another way of describing flipping is that it moves the corner point where the direction change takes place from its original location to the location diagonally opposite.
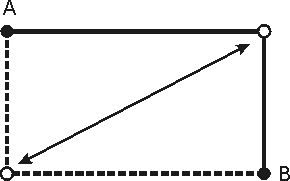
Figure 10: Flipping
Sliding
When a line connects two parallel lines rectangulary is it possibly to slide the line in one of the directions dictated of the two lines.
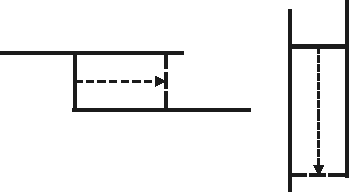
Figure 11: Sliding