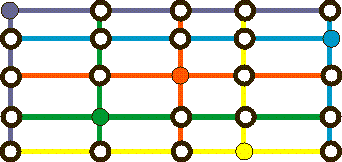
Figure 12: Hanan Grid.
Completed circles indicating the terminals. Hollow circles indicating possible Steiner points.
When Hanan in 1966 published the first paper solely devoted to the Rectilinear Steiner Tree Problem (RSTP), he gave the fundamental structural result known as the Hanan grid.
To draw a Hanan Grid:
Draw horizontal and vertical lines though all terminals in the set Z of terminals.
Let H(Z), called the Hanan Grid, denote the grid that is obtained.
Let IH(Z) be the set of intersections in H(Z). If n = |Z|, then the number of intersections is O(n2).
Note that the terminals is part of I(Z)
In fig.12 the terminals are colored in distinct colors. The lines drawn from every terminal is colored in the same color as the terminal.

Theorem 2.5
There exists an SMT for Z such that every Steiner point belongs to IH(Z)
The importance of this theorem is that we only need to consider a polynomial number of Steiner points candidates. Namely the O(n2) intersection points in the Hanan grid.
This means that there exist short certificates of optimal solutions. Thus we have proven that the RSTP is in NP.
Note: This is in contrast with the Euclidean Steiner tree problem for which this question is still unsettled.