History

The Steiner Minimum Tree problem has the last forty years gotten widespread attention, but its history goes back four centuries. Although many of the scientists in the early years did not publish their work in books or articles, the notes and letters they have left, gives us today a possibility to trace the evolution of the Steiner Minimum Tree problem.

Pierre de Fermat (1601-1665)
In the early 1600, Fermat proposed the following problem: given 3 points in the plane, find a fourth point T such that the length from this point to the 3 given points is minimal.
The original treatment of the problem considered only triangles with acute angles, for which T must be an interior point. Therefore, a discussion of the relative position of T with respect to the triangle did not emerge.
Before 1640, Torricelli solved this problem and the point has since been known as the Torricelli-point. Torricelli's method was to construct equilateral triangles on each side of the triangle made up by the original points. Circles circumscribing the equilateral triangles intersect in the point that is sought (Figure 1). This point is called the Torricelli point.

Evangelista Torricelli (1608-1647)

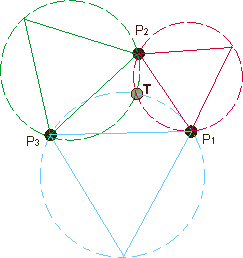
Figure 1: Torricelli method.

Bonaventura Francesco Cavalieri (1598-1647)
Cavalieri in his "Exercitationes geometricae" of 1647, showed that the sides of the given triangle subtend angles of 120 degrees from the Torricelli point.
Thomas Simpson proved in his "Doctrine and Application of Fluxions" (London, 1750), that the three lines joining the outside vertices of the equilateral triangles defined above, to the opposite vertices of the given triangle intersect in the Torricelli point. These three lines are called Simpson lines (Figure 2). He is also credited as being the first to discuss the weighted variant of the problem, and having generalized the problem to n points.

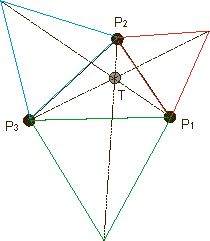
Figure 2: Simpson’s method.

A method proposed by the mathematicians of the mid seventeenth century for the three point problem is illustrated in Figure 3. This method stated that in order to calculate the Steiner Point given points A, B and C, you first construct an equilateral triangle (ABX) using the longest edge between two of the points (AC) such that the third (B) lies outside the triangle. A circle is circumscribed around the triangle, and a line is constructed from the third point (B) to the far vertex of the triangle (X). The location of the Torricelli point (T) is the intersection of this line (BX) with the circle.

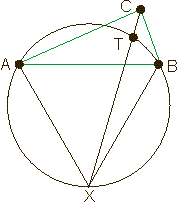
Figure 3: Method used in mid 1700.

In 1834, Heinen showed that the Toricelli point is only the solution to Fermat's problem if the triangle of the three given points does not contain an angle larger than 120 degrees.
The Steiner minimum tree problem is an indirect generalization. Recent research on mathematical history showed that Gauss first studied this generalization (i.e., the Steiner minimum tree).

Johann Carl Friedrich Gauss (1777-1855)
On March 19th., 1836 the astronomer Schuhmacher wrote a letter to his friend the mathematician Gauss in which he was surprised about a specific case of the Fermat problem. He considered four points v₁, v₂, v₃, v₄ in the plane which forms a quadrilateral such that the segments v₁v₂ and v₃v₄ are parallel and the lines of the segments v₁v₃ and v₂v₄ meet in one point v outside. Now the Torricelli point T of these four points is the intersection point of the diagonals v₁v₄ and v₂v₃ Schuhmacher did not understand the fact that, if the segment v₃v₄ runs to the point v the point q runs in the same way to v, but this cannot be, since the Torricelli point of three points is not necessarily one of the given points.

In an answer, March 21, Gauss answered that Schuhmacher did not consider the Fermat problem, he looked for a solution of:

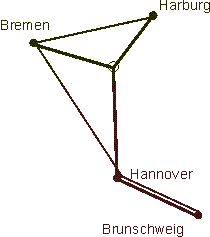
Figure 4: Gauss's question

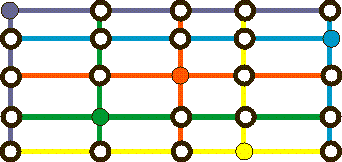
Figure 5: Hanan Grid.

The Manhattan SMT is today normally known as the rectilinear Steiner minimum tree, or just RSMT.

In 1968 Gilbert and Pollak, in theirs article "Steiner minimal trees", linked the length of the SMT to the length of a MST. It was already known that the length of an MST (minimum spanning tree) is an upper bound for the length of an SMT, but their conjecture stated that the length of an SMT in the Euclidean plane would never be any shorter than sqr(3)/2 times the length of an MST. This conjecture was first proved in 1990 by D.-Z. Du and F.K. Hwang in Proceedings of National Academy of Sciences U.S.A., 87.

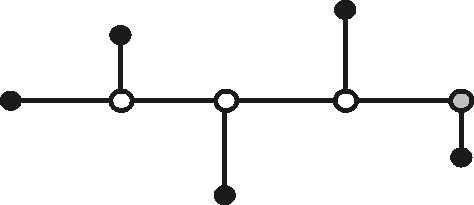
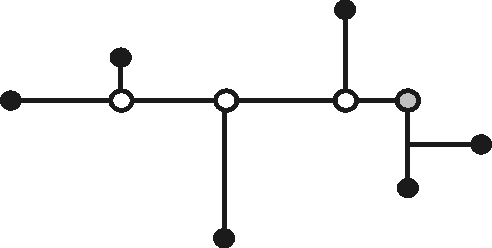
In 1976 gave F.K. Hwang a precise description of the topology of rectilinear FST (Full Steiner Tree, a Steiner tree where all terminals is leafs) in On Steiner minimal trees with rectilinear distance. He proved that there always exists an SMT for which every FST is one of two generic forms shown in Fig.5.
He also proved that the Steiner ratio for the rectilinear Steiner problem is 2/3.

Figure 6: Hwang topology - type I		Figure 7: Hwang topology - type II

M.R. Garey, R.L. Graham, and D.S. Johnson proved in "The complexity of computing Steiner minimum trees" in 1977, that the Rectilinear Steiner problem is NP-complete.

Industry

The RSMT problem has numerous applications in the area of VLSI design automation as well as printed circuit board layout. For example, an RSMT for a set of electron devices can be used as a lower bound estimate on the wire length of a route connecting all of the devices together. An RSMT of the points represents only a lower bound since a real interconnect satisfies additional constraints requiring it to avoid other obstacles that are also present on the chip. Recent work by Ganley treated such obstacle avoiding RSMTs directly. In addition to global wire length estimation, RSMTs have also been used to evaluate the merit of functional block placements in floorplanners such as the MONDRIAN system. Wagner reduces certain cases of parallel expression evaluation to the RSMT problem. The ESMT problem has applications in the design of electrical power distribution Networks, oil and natural gas pipelines and other network design problems.