Hwang topology

Hwang

In sliding and flipping we saw, what it means to slide and flip, and what the consequences are. A SMT/FST will have the same length after a slide or flip, as it had before. One of the reasons to introduce sliding and flipping, is that when computing SMTs there are an infinite amount of solutions. Even though the amount of solutions is dramatically reduced by introducing Hanan grid, several solutions still exists.

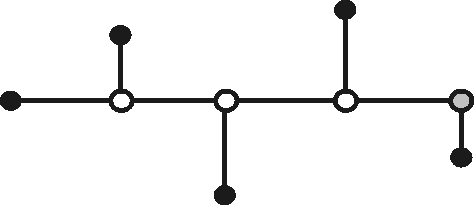
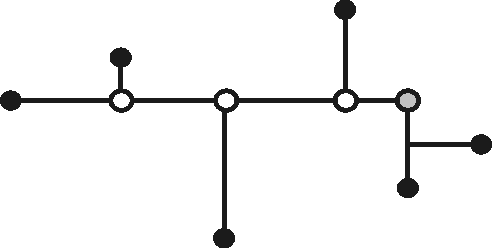
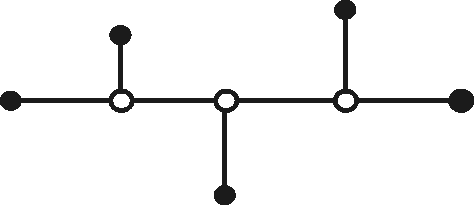
To be able to find a single 'unique' solution, we introduce Hwang-topology FSTs. A Hwang-topology FST has a special form and some special properties. A Hwang-topology FST consist of a long leg and (in traditional form) a short leg. The long leg, which in one end must have a Terminal, and in the other end a corner point, consists of zero or more Steiner points, which must be T-points. The short leg, has in one end the same corner point as the long leg, and the other end, always a Terminal. The short leg can have zero or one T-point going the same way as the backbone. Every terminal in a FST is a leaf i.e. has degree 1.

Ex. if the long leg is going east (i.e. towards your right), and if the first terminal is to the north of the backbone, then the second must be to the south of the backbone, the third to the north, etc. If the short leg has a T-point it must be going east.

The first property says that the incident segments alternate along the backbone. See the applet under 'Hwang construct' for some examples that shows why Hwang-topology alternate along the backbone. Note; Long leg and short leg has nothing to do with geometric length, rather that the long leg has zero or more alternating segments, whereas the short leg has zero or one segment.
For the property that the short leg has at most one incident segment, see the applet under 'Short leg T-point count'.
For a formal proof see the article: 'The rectilinear Steiner Tree problem: A tutorial' by Martin Zachariasen, 2001. As a note can be mentioned that the short leg is always opposite the last alternating segment on the backbone.

It is recommended to use 'step' the first time seeing the applet, since the explaining text displays quite rapid.

Notes to the applet

In 'Hwang construct' if Sb does not exist, the same techniques, as used in the applet, can be used to show this. The same goes if |uv| is vertical.

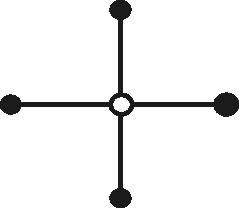
In the applet are shown some informal proofs on, why Hwang-topology looks as it does, so now we show how the FSTs actually looks. There exist two different types: Type (i) and type (ii). Type (i) has furthermore two degenerate types, named type (i') and type (i'').

**Figure 1:** Hwang-topology FSTs
(a) Type (i)	(b) Type (ii)	(c) Type (i')	d) Type (i'')

The amount of T-points on the backbone is naturally dependent of the actual situation, so figure 13 only demonstrates how they could look if Type (i), type (i') type (ii) has three alternating segments. Figure 13d illustrates the only possible situation for type (i'') except from the length of the segments, which is situation dependent.

As a last property of Hwang-topology to be mentioned here, is that the geometric length of a type (i) short leg must be shorter then all the segments on the same side. For a type (ii), the length between the corner point and the segment must be shorter than the segments on the same side. See applet under 'Max. short leg length'.